Cota: Es un número que es el mayor o menor que cualquier elemento de un conjunto.
los límites en el infinito se representan como casos especiales en los cuales la función f(x) crece o decrece sin cota cuando x se aproxima a los valores dados para determinar estos límites se divide el numerador y denominador de la función racional entre el grado mayor del polinomio.
A partir de este proceso se pueden dar los siguientes casos:
Ejercicios hechos en khan academy:
1)
2)
3)
Ejercicios:
1)
Efectuamos el producto en el denominador:

Como el límite es al infinito y el grado del polinomio del polinomio del denominador es mayor que el del numerador:

2)

El límite es al infinito.
Los monomios que más influencia tienen en el límite son los de grado mayor. Por ello, podemos escribir la siguiente igualdad (quitando los monomios de grado pequeño del radicando):

De este modo, al escribir la raíz como una potencia, tenemos un cociente de polinomios de mismo grado:

3)
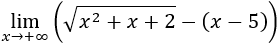
Sustituimos el infinito para ver que obtenemos una indeterminación

Como tenemos una resta de infinitos, vamos a multiplicar y a dividir por el conjugado. Recordemos que el conjugado de a+b es a-b.
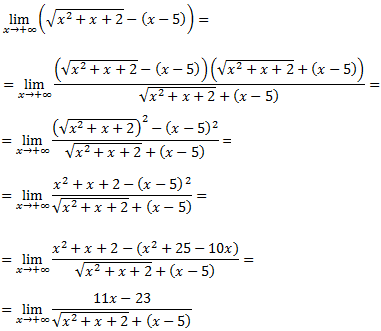
Notemos que hemos conseguido un polinomio (de grado 1) en el numerador y el denominador no es un problema ya que se trata de una suma (lo sería en caso de ser una resta). Nos quedamos con el monomio de grado mayor del radicando para obtener un cociente de polinomios.
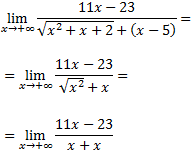
Luego tenemos un cociente de polinomios del mismo grado y el límite es al infinito, por tanto,
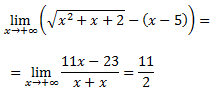
4)

Podemos considerar la función como un polinomio (transformando la raíz en una potencia).

Ya que 5 > 3/2.

5)

Efectuamos el producto en el denominador:

Como el límite es al infinito y el grado del polinomio del polinomio del denominador es mayor que el del numerador:









No hay comentarios:
Publicar un comentario