Limites Unilaterales

Vídeo de explicación:

Hay casos en que las funciones no están definidas (en los reales) a la izquierda o a la derecha de un número determinado, por lo que el límite de la función cuando x tiende a dicho número, que supone un intervalo abierto que contiene al número, no tiene sentido.

                          

             

               

Tomado de la siguiente pagina:http://ed21.webcindario.com/LimitesYContinuidad/limites_unilaterales.htm#Límites_unilaterales

limites unilaterales a través de gráfica:





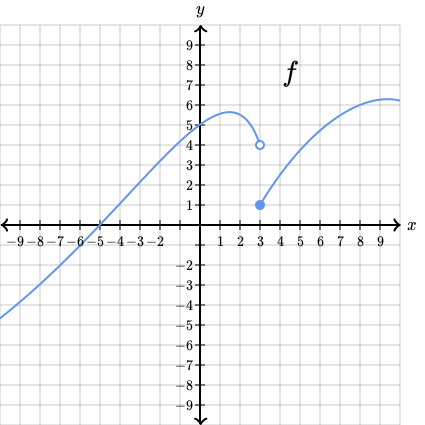
Observa solamente la parte de la gráfica que está a la izquierda de la recta vertical $x=3$x, equals, 3.

Conforme $x$x se aproxima a $3$3 —por ejemplo, $x=2.9$x, equals, 2, point, 9, $2.99$2, point, 99,$2.999$2, point, 999, y así sucesivamente— observa dónde están los puntos$(x,f(x))$left parenthesis, x, comma, f, left parenthesis, x, right parenthesis, right parenthesis sobre la gráfica.

Conforme $x$x se aproxima a $-3$minus, 3 por la izquierda, el valor límite de$f(x)$f, left parenthesis, x, right parenthesis parece ser $4$4.











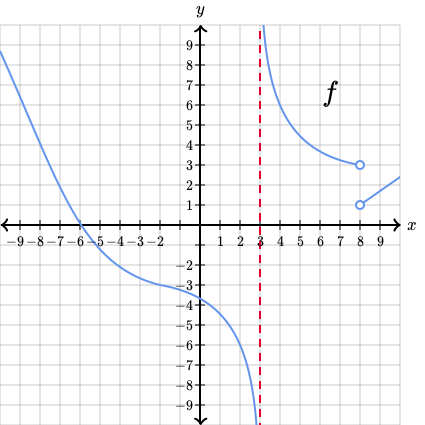
Observa solamente la parte de la gráfica que está a la derecha de la recta vertical $x=3$x, equals, 3.

Conforme $x$x se aproxima a $3$3 —por ejemplo, $x=3.1$x, equals, 3, point, 1, $3.01$3, point, 01,$3.001$3, point, 001, y así sucesivamente— observa dónde están los puntos$(x,f(x))$left parenthesis, x, comma, f, left parenthesis, x, right parenthesis, right parenthesis sobre la gráfica.

El valor límite de $f(x)$f, left parenthesis, x, right parenthesis conforme $x$x se aproxima a $3$3 por la derecha parece ser $\infty$infinity.